Weakly Convex Optimization

Introduction

This post will explain in brief details the concept of weak convexity and the methods used to solve some important weakly convex problems such as Robust Matrix Sensing and Robust Phase Retrieval.

Many of the descriptions here will be very high-level and intended for non-technical readers. For additional explanation and in-depth mathematical analysis of the algorithms and proofs for their properties please visit this link

Weak Convexity

Firstly, a general notion and description of weak convexity is needed. In order to stay in the realm of sanity, we can view a weakly convex function as a function that can be made covex by adding a second, parameterized term to it. The key idea behind adding such a term is find a way to measure the progress of an algorithm by tracking a surrogate optimality measure that is easier to work with.

Moreau Envelope

The Moreau Envelope is the surrogate measure that will enable us to exactly that. When we apply the moreau envelope to a weakly convex function, it gives us a continiously differentiable function that approximates the original function from below and more importantly, with proof provided in the paper, we can see that the problem of minimizing the original function is equivalent to minimizing the envelope which is always a smooth optimization problem.

Proximal Operators and Algorithms

An important concept that is needed to understand the algorithms discussed in the paper is the proximal operator.

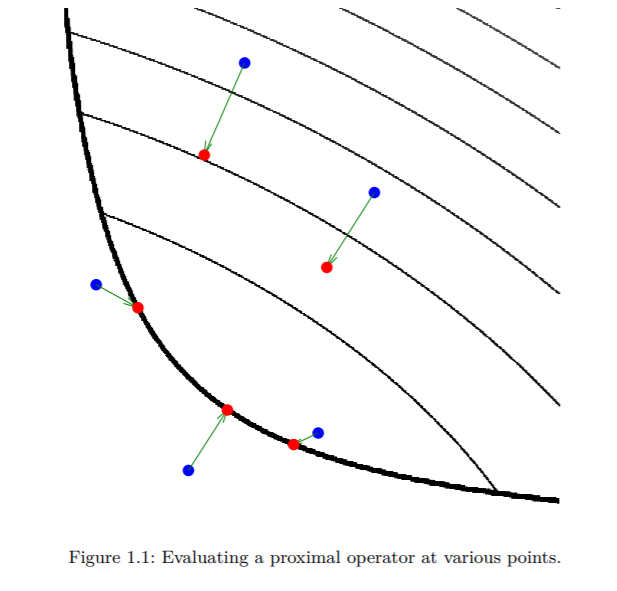
The figure illustrates how the proximal operator works: the thick black line indicates the boundary of the domain of the convex function \(f\). Applying the operator to the blue points moves them to the corresponding red points. The three points in the domain of the function stay in the domain and move towards the minimum of the function, while the other two move to the boundary of the domain and towards the minimum of the function. The parameter \(\lambda\) controls the extent to which the proximal operator maps points towards the minimum of \(f\).

A proximal algorithm solves convex optimization problems using the proximal operators of the objective terms. For example, the proximal minimization algorithm, minimizes a convex function \(f\) by repeatedly applying \(prox_f\) to some initial point.

Incremental Algorithms and Convergence Rates

Incremental algorithms are suited for solving the finite sum optimization problem:

\[\min_{x \in \mathbb{R}^n}f(x)=\sum_{i=1}^m f_i(x)\]

So the question is what are incremental algorithms? In short, if you know stochastic algorithms, then you will also know how incremental algorithms work. The only difference between the two, is how they sample the given data: stochastic algorithms randomly choose a function from the set, whereas the incremental algorithms choose them in an iterative fashion, starting from the first component function and ending with the last one in each epoch.

Although not intuitive at first glance why would these different sampling techniques make a difference, careful examination shows us that stochastic algorithms might suffer from selection bias, or simply oversampling and undersampling some composite functions with respect to the rest. Ultimatelly, they fulfill the same goal but incremental algorithms tend to converge faster because of this advantage.

Three different incremental algorithms (Sub-gradient, proximal point and prox-linear) their stochastic counter-parts, and their respective convergence rates are analyzed in more detail in the paper if you are interested in the maths behind the different approaches.

Examples

Robust Matrix Sensing

Low-rank matrices have a very broad application in many areas such as Computer Vision and Machine Learning. A very important computational task is to recover these kind of matrices from a small number of linear measurements arbitrarily corrupted with outliers. This task naturally admits a weakly convex loss function that can be solved with the approaches talked about above.

Robust Phase Retrieval

Like the previous task, robust phase retrieval similarly tries to recover a signal from its magnitude-wise measurements (Think loudness of sound) that are randomly corrupted with outliers. Given some strong assumptions, it can be proven that there exists a set of optimizers to the carefully constructed loss function.

Experiments

In the paper, we replicated some results obtained by pioneers in this weak convexity area and discussed them in more detail. The key take-away from the experiments was to show two important properties of the incremental algorithms:

1. Like stated before, incremental algorithms show superior convergence rates with regards to their stochastic counterparts and;
2. Not covered in this post, incremental algorithms show better flexibility in the choice of hyperparameters which is really important to further the robustness of general algorithms.

Conclusion

In this brief post, and in-depth paper, we show the more recent advances in the weak convexity field, and in the field of optimization in general. These steps in defining a new set of weakly convex problems are the first of I think many in finding a general approach for solving non-convex problems in general.